연결 리스트 연산 - 원소 삽입
def insertAt(self, pos, newNode):
1) pos가 가리키는 위치에 (1 <= pos <= nodeCount + 1)
2) newNode를 삽입하고
3) 성공/실패에 따라 True / False 를 리턴
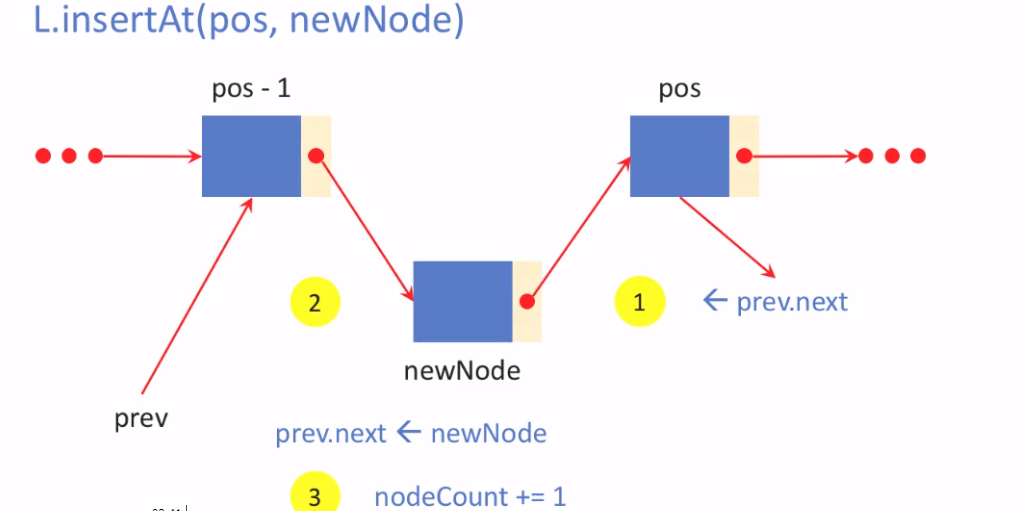
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
코드 구현 주의사항
(1) 삽입하려는 위치가 리스트 맨 앞일 때
-> prev 없음
-> Head 조정 피료
(2) 삽입하려는 위치가 리스트 맨 끝일 때
-> Tail 조정 필요
(3) 빈 리스트에 삽입할 때?
-> (1), (2) 두 조건에 의해 처리됨
#참고: 전체 코드
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr is not None:
s += repr(curr.data)
if curr.next is not None:
s += ' -> '
curr = curr.next
return s
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr is not None:
result.append(curr.data)
curr = curr.next
return result
def concat(self, L):
self.tail.next = L.head
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount연결 리스트 원소 삽입의 복잡도
- 맨 앞에 삽입하는 경우: O(1)
- 중간에 삽입하는 경우: O(n)
- 맨 끝에 삽입하는 경우: O(1)
연결 리스트 연산 - 원소 삭제
def popAt(self, pos):1) pos가 가리키는 위치의 (1<= pos <= nodeCount)
2) node를 삭제하고
3) 그 node의 데이터를 리턴

코드 구현 주의사항
(1) 삭제하려는 node가 맨 앞의 것일 때
-> prev 없음
-> Head 조정 필요
(2) 리스트 맨 끝의 node를 삭제할 때
-> Tail 조정 필요
(3) 유일한 노드를 삭제할 때
-> (1), (2) 두 조건에 의해 처리되는가?
(4) 삭제하려는 node가 마지막 node일 때, 즉 pos==nodeCount인 경우?
-> 한 번에 처리할 수 없다 (prev를 찾을 방법이 없으므로)
-> 앞에서부터 찾아와야 함
연결 리스트 원소 삭제의 복잡도
- 맨 앞에서 삭제하는 경우: O(1)
- 중간에서 삭제하는 경우: O(n)
- 맨 끝에서 삭제하는 경우: O(n)
연결 리스트 연산 - 두 리스트의 연결
def concat(self, L):1) 연결 리스트 self의 뒤에
2) 또 다른 연결 리스트인 L을 이어 붙임
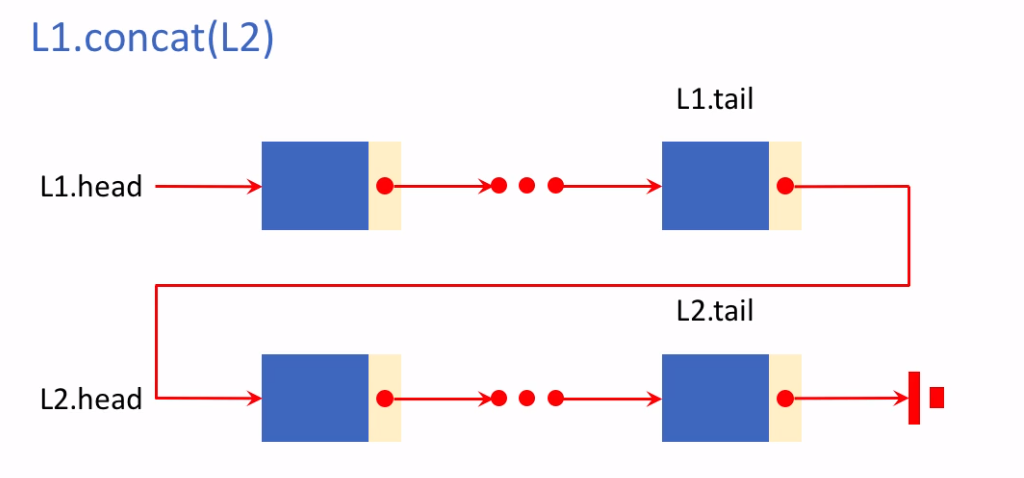
def concat(self, L):
self.tail.next = L.head
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount실습 과제 - 연결 리스트 노드 삭제
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
raise IndexError
if pos == 1:
curr = self.head
if self.nodeCount == 1:
self.head = None
self.tail = None
else:
self.head = curr.next
self.nodeCount -= 1
return curr.data
else:
prev = self.getAt(pos - 1)
curr = prev.next
if pos == self.nodeCount:
prev.next = None
self.tail = prev
self.nodeCount -= 1
return curr.data
else:
prev.next=curr.next
self.nodeCount -= 1
return curr.data
def traverse(self):
result = []
curr = self.head
while curr is not None:
result.append(curr.data)
curr = curr.next
return result
def solution(x):
return 0
* 프로그래머스의 '어서와! 자료구조와 알고리즘은 처음이지?' 강의를 듣고 정리하였습니다.
'알고리즘 강의' 카테고리의 다른 글
| [알고리즘 강의] 파트10. 양방향 연결 리스트(Doubly Linked Lists) (0) | 2021.07.15 |
|---|---|
| [알고리즘 강의] 파트9. 연결 리스트(Linked Lists) (3) (0) | 2021.07.15 |
| [알고리즘 강의] 파트7. 연결 리스트(Linked Lists) (1) (0) | 2021.07.14 |
| [알고리즘 강의] 파트6. 알고리즘의 복잡도(Complexity of Algorithms) (0) | 2021.07.13 |
| [알고리즘 강의] 파트5. 재귀 알고리즘(Recursive Algorithms) 응용 (0) | 2021.07.13 |



