시간 복잡도(Time Complexity)
문제의 크기와 이를 해결하는데 걸리는 시간 사이의 관계
공간 복잡도(Space Complexity)
문제의 크기와 이를 해결하는데 필요한 메모리 공간 사이의 관계
평균 시간 복잡도(Average Time Complexity)
임의의 입력 패턴을 가정했을 때 소요되는 시간의 평균
최악 시간의 복잡도(Worst-case Time Complexity)
가장 긴 시간을 소요하게 만드는 입력에 따라 소요되는 시간
Big-O Notation
- 점근 표기법(asymptotic notation)의 하나
- 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현(알고리즘의 복잡도를 표현할 때 흔히 쓰임)
- O(logn), O(n), O(n^2), O(2^n)
- 입력의 크기가 n일 때,
- O(logn) - 입력의 크기의 로그에 비례하는 시간 소요
- O(n) - 입력의 크기에 비례하는 시간 소요
- 계수는 그다지 중요하지 않음
선형 시간 알고리즘 - O(n)
예: n개의 무작위로 나열된 수에서 최댓값을 찾기 위해 선형 탐색 알고리즘을 적용
- 최댓값 - 끝까지 다 살펴보기 전까지는 알 수 없음
- Average case:O(n)
- Worst-case:O(n)
로그 시간 알고리즘 - O(logn)
예: n개의 크기순으로 정렬된 수에서 특정 값을 찾기 위해 이진 탐색 알고리즘을 적용
이차 시간 알고리즘 - O(n^2)
예: 삽입 정렬(insertion sort)
- Best case: O(n) - 이미 정렬된 상태
- Worst case: O(n^2) - 역순으로 정렬된 상태

보다 나은(낮은) 복잡도를 가지는 정렬 알고리즘
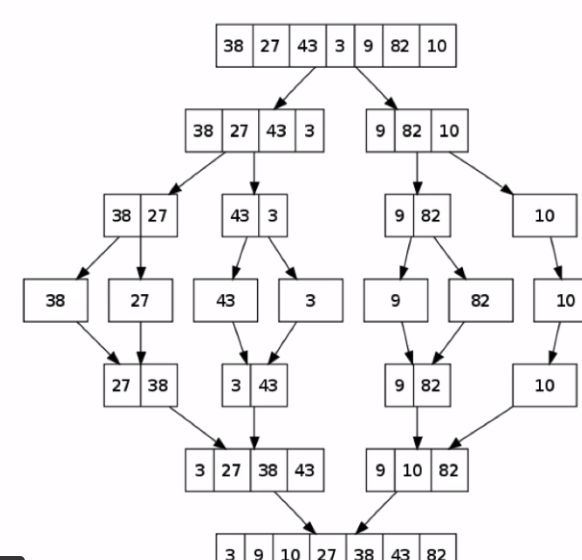
예: 병합정렬(merge sort) - O(nlogn)
참고: 입력 패턴에 따라 정렬 속도에 차이가 있지만 정렬 문제에 대해 O(nlogn)보다 낮은 복잡도를 갖는 알고리즘은 존재할 수 없음이 증명되어 있음
(1) 정렬한 데이터를 반씩 나누어 각각 정렬시킨다.
-> O(logn)
(2) 정렬된 데이터를 두 묶음씩 한데 합친다.
-> O(n)
(3) 결론적으로 O(nlogn)
꽤나 복잡한 문제
유명한 예: 배낭 문제(Knapsack Problem)

* 프로그래머스의 '어서와! 자료구조와 알고리즘은 처음이지?' 강의를 듣고 정리하였습니다.
'알고리즘 강의' 카테고리의 다른 글
| [알고리즘 강의] 파트8. 연결 리스트(Linked Lists) (2) (0) | 2021.07.14 |
|---|---|
| [알고리즘 강의] 파트7. 연결 리스트(Linked Lists) (1) (0) | 2021.07.14 |
| [알고리즘 강의] 파트5. 재귀 알고리즘(Recursive Algorithms) 응용 (0) | 2021.07.13 |
| [알고리즘 강의] 파트4. 재귀 알고리즘(Recursive Algorithms) 기초 (0) | 2021.07.13 |
| [알고리즘 강의] 파트3. 배열 더 알아보기: 정렬과 탐색(Sorting & Searching) (0) | 2021.07.13 |

