힙 (Heap) 이란?
이진 트리의 한 종류 (이진 힙 - binary heap)
1. 루트 (root) 노드가 언제나 최댓값 또는 최솟값을 가짐 (모든 서브트리의 루트에서)
- 최대 힙 (max heap), 최소 힙 (min heap)
2. 완전 이진 트리여야 함
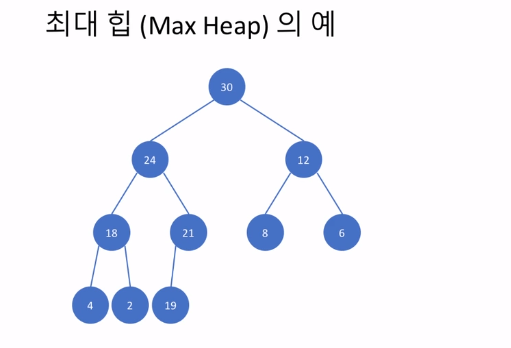
재귀적으로도 정의됨
(어느 노드를 루트로 하는 서브트리도 모두 최대 힙)
이진 탐색 트리와의 비교
1. 원소들은 완전히 크기 순으로 정렬되어 있는가?
이진탐색: YES, 힙 NO
2. 특정 키 값을 가지는 원소를 빠르게 탐색할 수 있는가?
이진탐색: YES, 힙 NO
3. 부가의 제약 조건은 어떤 것인가?
힙 - 완전이진트리
최대 힙(Max Heap)의 추상적 자료구조
연산의 정의
- __init__() : 빈 최대 힙을 생성
- insert(item) : 새로운 원소를 삽입
- remove() : 최대 원소 (root node)를 반환 (그리고 동시에 이 노드를 삭제)
데이터 표현의 설계
배열을 이용한 이진 트리의 표현
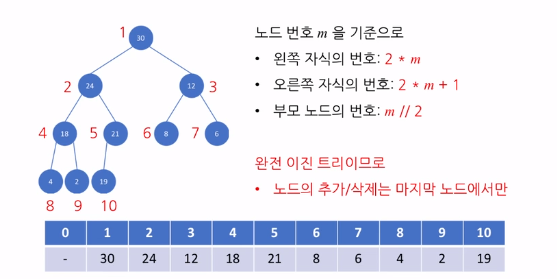
코드의 구현 - 빈 힙 생성
class MaxHeap:
def __init__(self):
self.data = [None] # 0번 index에는 None
최대 힙에 원소 삽입
1. 트리의 마지막 자리에 새로운 원소를 임시로 저장
2. 부모 노드와 키 값을 비교하여 위로, 위로, 이동
최대 힙에 원소 삽입 - 복잡도
원소의 개수가 n인 최대 힙에 새로운 원소 삽입
-> 부모 노드와의 대소 비교 최대 횟수: log2n
최악 복잡도 O(logn)의 삽입 연산
실습 과제 - 삽입 연산의 구현
class MaxHeap:
def __init__(self):
self.data = [None]
def insert(self, item):
self.data.append(item)
idx = len(self.data) - 1
while (idx//2 >= 1) and (item > self.data[idx//2]):
self.data[idx], self.data[idx//2] = self.data[idx//2], self.data[idx]
idx = idx//2
def solution(x):
return 0
* 프로그래머스의 '어서와! 자료구조와 알고리즘은 처음이지?' 강의를 듣고 정리하였습니다.
'알고리즘 강의' 카테고리의 다른 글
| [알고리즘 강의] 파트23. 힙(Heaps) (2) (0) | 2021.07.25 |
|---|---|
| [알고리즘 강의] 파트21. 이진 탐색 트리(Binary Search Trees) (2) (0) | 2021.07.24 |
| [알고리즘 강의] 파트20. 이진 탐색 트리(Binary Search Trees) (1) (0) | 2021.07.22 |
| [알고리즘 강의] 파트19. 이진 트리 - 넓이 우선 순회(breadth first traversal) (0) | 2021.07.22 |
| [알고리즘 강의] 파트18. 이진 트리(Binary Trees) (0) | 2021.07.21 |


