이진 트리의 추상적 자료구조
연산의 정의
- size(): 현재 트리에 포함되어 있는 노드의 수를 구함
- depth(): 현재 트리의 깊이 (또는 높이; height) 를 구함
- 순회 (traversal)
이진 트리의 구현 - 노드 (Node)

class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
이진 트리의 구현 - 트리 (Tree)
class BinaryTree:
def __init__(self, r):
self.root = r
이진 트리의 구현 - size()
- 재귀적인 방법으로 쉽게 구할 수 있음!
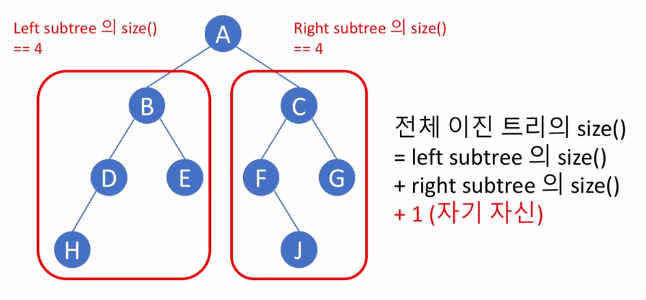
class Node:
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l + r + 1class BinaryTree:
def size(self):
if self.root:
return self.root.size()
else: # empty tree
return 0
이진 트리의 구현 - depth()
- 재귀적인 방법으로 쉽게 구할 수 있음!

이진 트리의 순회 (Traversal)
- 깊이 우선 순회 (depth first traversal)
ㄴ 중위 순회 (in-order traversal)
ㄴ 전위 순회 (pre-order traversal)
ㄴ 후위 순회 (post-order traversal)
- 넓이 우선 순회 (breadth first traversal)
중위 순회 (in-order traversal)
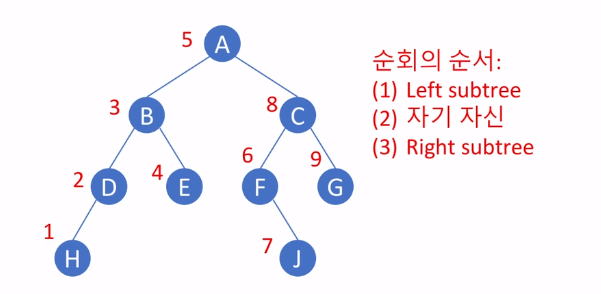
class Node:
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return traversalclass BinaryTree:
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
전위 순회 (Pre-order Traversal)
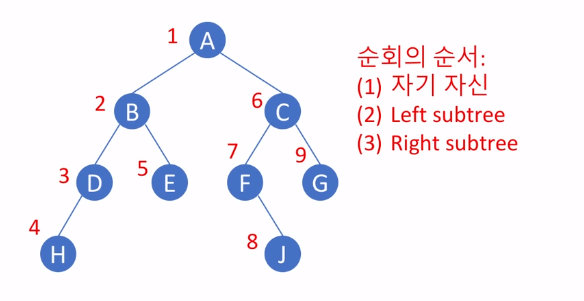
후위 순회 (post-order traversal)

실습 과제 - 코드는 깃헙에
1) 이진트리의 depth() 연산 구현 - lab18-1.py
2) 이진트리의 전위순회 연산 구현 - lab18-2.py
3) 이진트리의 후위순회 연산 구현 - lab18-3.py
'알고리즘 강의' 카테고리의 다른 글
| [알고리즘 강의] 파트20. 이진 탐색 트리(Binary Search Trees) (1) (0) | 2021.07.22 |
|---|---|
| [알고리즘 강의] 파트19. 이진 트리 - 넓이 우선 순회(breadth first traversal) (0) | 2021.07.22 |
| [알고리즘 강의] 파트17. 트리(Trees) (0) | 2021.07.21 |
| [알고리즘 강의] 파트16. 우선순위 큐(Priority Queues) (0) | 2021.07.19 |
| [알고리즘 강의] 파트15. 환형 큐(Circular Queues) (0) | 2021.07.19 |


